Pavel's Puzzles

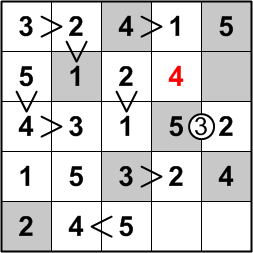
This is the example puzzle exactly as presented on the ænigma paper. We are given that we should place one of the digits 1 through 5 in each square of the grid such that (a) there is exactly one of each digit in each row and column, (b) squares that share a less-than or greater-than sign contain numbers that satisfy that inequality, and (c) squares that share a circled number contain digits that differ by exactly that amount.

As in all of my ænigmas, the individual deductions involved in solving this puzzle will all be relatively straightforward; the difficulty lies in finding those deductions in the first place. One way to begin is by searching the grid for a single row or column where all, or almost all, of the squares are involved in some kind of a constraint; the hope is that only one square's constraints will allow some specific digit.

To satisfy all of the inequalities, the 1 can only be placed in one square in the middle column: the exact center of our grid.

Now let us turn our attentions to the middle row of our grid. With the 1 in this row having been placed, there is only one pair of digits that could satisfy the circled-three constraint shared by the last two squares: those squares must contain a 2 and a 5, in one order or the other.

Staying in that central row, we now know, at least roughly, where the digits 1, 2, and 5 must be placed: they'll fill the rightmost three squares of the row. That leaves only the two digits 3 and 4 to occupy the other two squares in that row, and because those squares share a greater-than sign, we can immediately place them precisely.

The 4 we've just placed is contrained to be less than the digit in the square above it. Since we are placing only the digits 1 through 5, there is but one way to satisfy that constraint: the upper square must contain a 5.

Consider the square in the upper-left corner of the grid. It begins a chain of three squares, as indicated by the red arrow, that are all linked by greater-than signs. That corner square's digit, therefore, must be strictly greater than at least two other digits in our repertoire. That is, it must be at least a 3.

Since the leftmost column of the grid already contains a 4 and a 5, the only remaining digit that is at least a 3 is the digit 3 itself, and that is what must therefore be placed in the corner square.

Of course, once that 3 has been placed at the head of a chain of three greater-than signs, there is only one way to fill in the remainder of that chain, with a 2 and a 1.

All but one of the squares in the second column of the grid are now either filled with digits or involved in some kind of constraint, so it has become a potentially fruitful place in which to search for our next deduction.

The only digit meeting these criteria, of course, is the 4, which implies that the digit to its right must be a 5.

There remains only one square unfilled in the second column. The only digit left to place there is the 5.

Let us now focus on the middle square in the top row of the grid. It cannot be a 2 or a 3, since its row already contains those digits, and it cannot be a 1 or a 5, since those digits have already been placed in its column.

That leaves, of course, only the 4 to occupy that square.

The square to the right of the 4 we just placed must contain a digit less than 4; since the 2 and 3 in that row are, as noted before, already in position, that square's digit clearly must be a 1. That leaves only the 5 to be placed in the final square in that row.

The 5 placed in the previous step has done us a great favor, finally resolving the 2/5 ambiguity we discovered early on in our efforts. The 5 in the middle row cannot be in the rightmost column now, since we've now already placed a 5 there, so it must be in the fourth column of that row, with the 2 in the final position.

Returning our attentions to the central column of the grid, let us consider where that column's 2 could possibly be placed. Could it appear in the fourth row? That square is constrained to be greater than the square to its right. If we placed the 2 there, then the square to its right would have to be the 1. But that would leave us with two 1's in that column, a violation of the rules.

We can thus confidently place the middle column's 2 in the second row, leaving only the 3 to occupy that remaining fourth row.

As noted earlier, the square we've just occupied with a 3 shares a greater-than sign with the square to its right. Since that neighboring square cannot contain a 1, we must place a 2 there.

Gentle reader, we are now entering the final stages of our solution! Consider the fourth row of the grid: its 4 cannot be in the first column, since that column already contains a 4, so it must be placed in the final column.

That, of course, leaves only the 1 to be placed in the first column of that fourth row.

The first column now lacks only a 2.

The second row as yet lacks a 4. It cannot be in the rightmost column, since that column already contains a 4, so it must be placed in the fourth column.

As is now familiar, we are forced to place the second row's missing 3 in the one remaining open position.

The fourth and fifth columns now each lack only one digit, both of which we can easily provide.

Here we pause for just a moment to savor our completed grid.

We are told to sum up the digits in each column that occupy shaded squares, and then to translate that sum into a letter using the traditional correspondence: 1 = A, 2 = B, and so forth. This is, of course, readily done, yielding one letter per column.