
Adalogical Ænigma #5Walkthrough of the Example PuzzleGreetings, gentle patron!
What follows is a detailed description of how one might go about solving the example puzzle shown on the ænigma paper. I hope that you find it useful. For a copy of the ænigma itself, along with an abundance of other solving aids, please return to the main page for this ænigma.
Dedicated to your puzzle enjoyment,
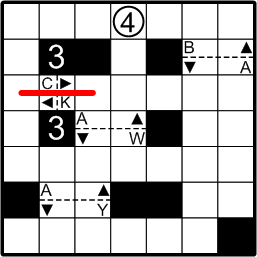
 This is the example puzzle exactly as presented on the ænigma paper. We are given that we should draw a single looped slalom course that begins and ends at the circled number, passes through each dotted-line ‘gate’ in strict, ascending numerical order, and never crosses or even touches itself. Only some of the gates are actually labelled with their numbers, however; the rest of the labels are for us to determine. Finally, we are told that our slalom path mayn't turn while passing through a gate.
This is the example puzzle exactly as presented on the ænigma paper. We are given that we should draw a single looped slalom course that begins and ends at the circled number, passes through each dotted-line ‘gate’ in strict, ascending numerical order, and never crosses or even touches itself. Only some of the gates are actually labelled with their numbers, however; the rest of the labels are for us to determine. Finally, we are told that our slalom path mayn't turn while passing through a gate.
Are the rules quite clear, then? Jolly good! Let's get started!
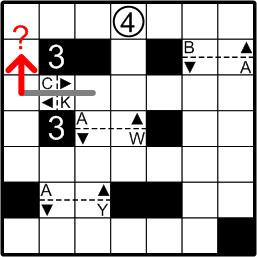
 When a gate is only one square wide, as is gate #3 in this grid, there can be only one way for the slalom course to pass through it.
When a gate is only one square wide, as is gate #3 in this grid, there can be only one way for the slalom course to pass through it.
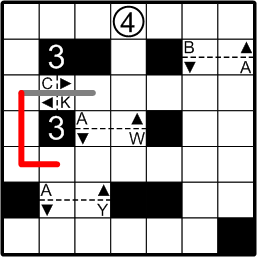
 Consider the left end of the path through gate #3. It must continue by turning either up or down. Could it indeed turn up, though? If it were to do so, it would have to continue all the way to the numbered circle, and that would imply that gate #3 was either the first or the last gate along the course. That cannot be, however: we know that there are four gates in all, and that our course passes through them in ascending numerical order. Thus, the path may not bend upwards here.
Consider the left end of the path through gate #3. It must continue by turning either up or down. Could it indeed turn up, though? If it were to do so, it would have to continue all the way to the numbered circle, and that would imply that gate #3 was either the first or the last gate along the course. That cannot be, however: we know that there are four gates in all, and that our course passes through them in ascending numerical order. Thus, the path may not bend upwards here.
 Now that we know the path turns downward from gate #3, we can trace out several squares of its path, since there are no potential branching points for some distance.
Now that we know the path turns downward from gate #3, we can trace out several squares of its path, since there are no potential branching points for some distance.
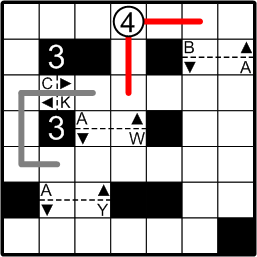 We are given that the course begins and ends at the circled number. If the course were to leave the number via the leftward path, it would encounter difficulty, since there would be no legal way for it to join the course already passing through gate #3. With that exit thus eliminated, only two exits remain: our path must make use of both of them, one to begin the course, and one to end it. We cannot yet say which is the beginning and which the ending, of course.
We are given that the course begins and ends at the circled number. If the course were to leave the number via the leftward path, it would encounter difficulty, since there would be no legal way for it to join the course already passing through gate #3. With that exit thus eliminated, only two exits remain: our path must make use of both of them, one to begin the course, and one to end it. We cannot yet say which is the beginning and which the ending, of course.
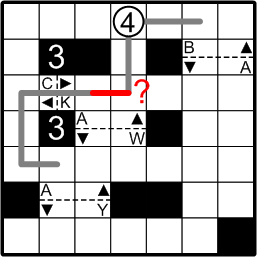 Could the two path ends to the right of gate #3 connect directly to one another, as shown? I am afraid not. Were they to do so, it would eliminate all possibility of the course later passing through the gate just below that point, in the centre of the grid. We are told that the course passes through all of the gates, so we can rule out this hypothesized connexion.
Could the two path ends to the right of gate #3 connect directly to one another, as shown? I am afraid not. Were they to do so, it would eliminate all possibility of the course later passing through the gate just below that point, in the centre of the grid. We are told that the course passes through all of the gates, so we can rule out this hypothesized connexion.
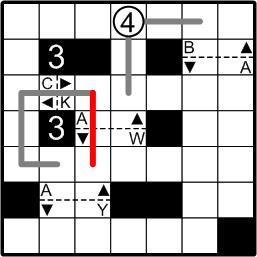 Since the path coming rightward through gate #3 may not continue straight ahead, we have no choice but to direct it downwards, straight through the gate below.
Since the path coming rightward through gate #3 may not continue straight ahead, we have no choice but to direct it downwards, straight through the gate below.
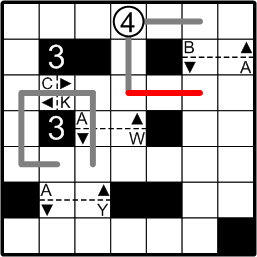 There are multiple locations in the grid now where we might continue our deductions, but let us continue working through the consequences of the hypothesis we ruled out two steps ago: now consider the path heading downward from the circled number. That path mayn't continue further downward, passing through the gate in the centre of the grid, since another section of the course already does so; our course must path through each gate exactly once. We thus must turn that path rightwards.
There are multiple locations in the grid now where we might continue our deductions, but let us continue working through the consequences of the hypothesis we ruled out two steps ago: now consider the path heading downward from the circled number. That path mayn't continue further downward, passing through the gate in the centre of the grid, since another section of the course already does so; our course must path through each gate exactly once. We thus must turn that path rightwards.
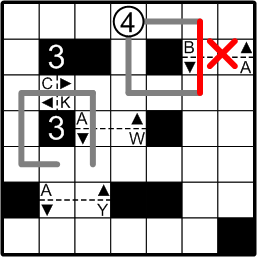 Now let us take up the path that travels rightward out of the circled number. It is quite clear that this path must soon pass through the nearby gate, in the upper-right portion of the grid. If it were to immediately do so, turning downward from its present ending point, it would be forced to form a tight little loop with the path exiting the bottom of the circled number, as shown here. We need our course to traverse all of the gates before returning to its starting point, so we must reject this option.
Now let us take up the path that travels rightward out of the circled number. It is quite clear that this path must soon pass through the nearby gate, in the upper-right portion of the grid. If it were to immediately do so, turning downward from its present ending point, it would be forced to form a tight little loop with the path exiting the bottom of the circled number, as shown here. We need our course to traverse all of the gates before returning to its starting point, so we must reject this option.
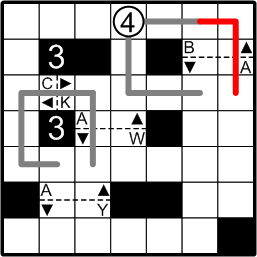 The foregoing argument leaves us with but one choice for where our uppermost path passes through the gate in question.
The foregoing argument leaves us with but one choice for where our uppermost path passes through the gate in question.
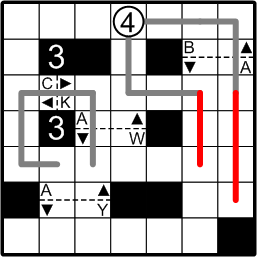 As we've established, the two path ends coming from the circled number mayn't yet connect, so each must continue as it may without touching the other.
As we've established, the two path ends coming from the circled number mayn't yet connect, so each must continue as it may without touching the other.
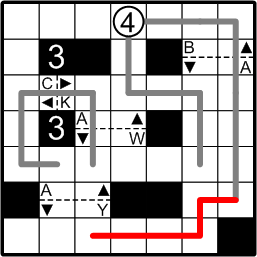 The rightmost path has only one way to wriggle through without making the forbidden connexion ...
The rightmost path has only one way to wriggle through without making the forbidden connexion ...
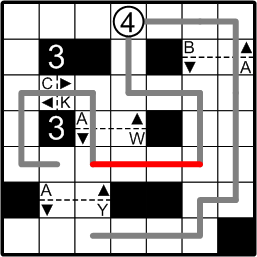 ... and that leaves the other end of that path but one way to continue.
... and that leaves the other end of that path but one way to continue.
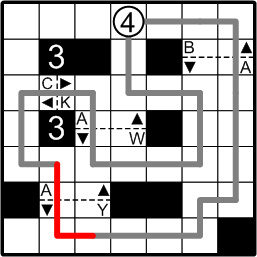 Finally we return to the end of the path that passed through gate #3. It has only the one option for how to proceed: it turns downward, through the bottom-most gate, whereupon it links up with the only remaining path end, thereby completing our slalom course. Well done!
Finally we return to the end of the path that passed through gate #3. It has only the one option for how to proceed: it turns downward, through the bottom-most gate, whereupon it links up with the only remaining path end, thereby completing our slalom course. Well done!
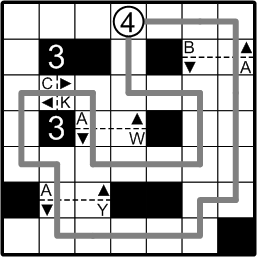 Here we pause for just a moment to catch our breaths after our exhilarating ski run!
Here we pause for just a moment to catch our breaths after our exhilarating ski run!
All that remains now is to discover this ænigma's final answer.
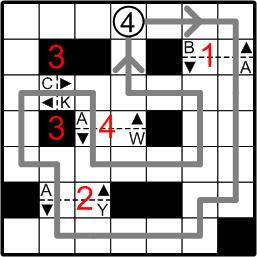 We are told to retrace our slalom course from start to finish, passing through the gates in ascending numerical order. Now that we have completed drawing our path, we can finally finish labelling all of the gates with their numbers.
We are told to retrace our slalom course from start to finish, passing through the gates in ascending numerical order. Now that we have completed drawing our path, we can finally finish labelling all of the gates with their numbers.
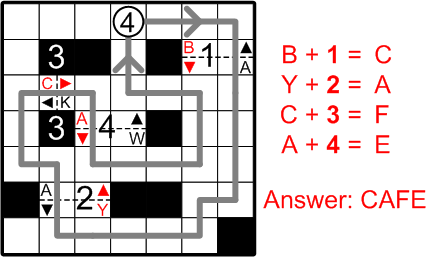 As we pass through each gate along our course, we are to collect the letter associated with the arrow indicating our direction of travel. We must then shift each letter forward in the alphabet by a number of steps equal to the label on that gate.
As we pass through each gate along our course, we are to collect the letter associated with the arrow indicating our direction of travel. We must then shift each letter forward in the alphabet by a number of steps equal to the label on that gate.
At gate #1, we collect a “B” and shift it forward by 1 letter, yielding a “C”.
Similarly, we collect a “Y” from gate #2, shifting it forward by 2 letters this time, wrapping around from “Z” to “A”.
Following this pattern with the remaining gates as shown, we end up spelling out our terribly apropos final answer word: “CAFE”.
Bravo, we've done it! Now return to your efforts on the original ænigma!
|
Shopping Cart |