Adalogical Ænigma #8

Walkthrough of the Example Puzzle

Greetings, gentle patron!
What follows is a detailed description of how one might go about solving the example puzzle shown on the ænigma paper. I hope that you find it useful. For a copy of the ænigma itself, along with an abundance of other solving aids, please return to the main page for this ænigma.
Dedicated to your puzzle enjoyment,
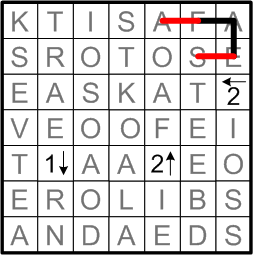
This is the example puzzle exactly as presented on the ænigma paper. We are given that we should blacken some of the squares in the grid (without ever creating two horizontally or vertically adjacent black squares). The arrows are each labelled with the exact count of black squares in the indicated direction along the same row or column. We are also to draw a single, connected loop (neither touching nor crossing itself) that passes through every single un-blackened square that does not contain an arrow.
Are the rules quite clear, then? Jolly good! Let's get started!
We begin by considering the square labelled “A” in the upper right-hand corner of the grid, asking ourselves the question, might it be blackened? If it were, then the square immediately below it, labelled “E” would (by the rule forbidding adjacent black squares) necessarily not be blackened. Then, because the loop we are drawing must pass through every non-blackened, non-arrow-laden square, that loop must somehow traverse that same “E” square. That, however, is an impossibility: the “E” square would have only one neighbor that could also participate in the loop, so the loop could not enter from one neighbor and leave by another as required.
We may thus safely conclude that the “A” square in that corner is not blackened.
Since the “A” square in that corner is not blackened, it must participate in the loop, and there is but a single way for the loop to traverse a corner square.
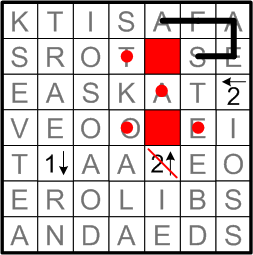
From that start on drawing the loop, we may safely extend both ends, each in the only direction available to it without allowing the path to close itself prematurely.
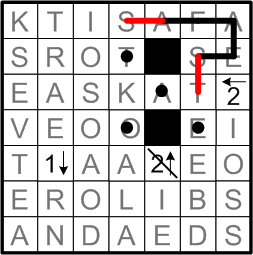
The up-pointing arrow labelled “2” indicates a requirement that there be two blackened squares above it in the same column. There now remains only one way to satisfy that requirement without placing black squares adjacently, so we may colour in those squares. We may also notate the further requirement that squares adjacent to black squares are not themselves blackened; we mark such known-non-black squares with a centered dot.
Finally, notice please how we have drawn a slash through the “2” arrow in question: we have fully discharged its requirements and need consider it no further during our solving.
This progress allows us to confidentally extend our nascent loop a bit further at each end.
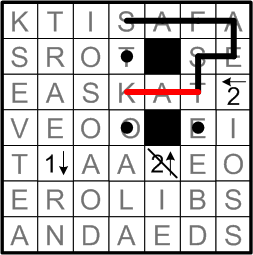The dotted square between the two black ones must participate in the loop, and it has exactly one way to do so.
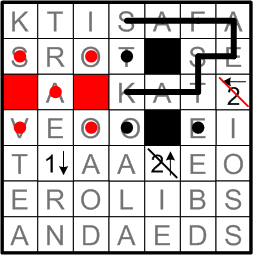By the same reasoning as above, we are now able with surety to identify the two black squares indicated by the arrow on the right edge of the grid. Once again, we also mark the neighboring squares that we now know not to be blackened, and we cross off the now-fully-satisfied arrow.
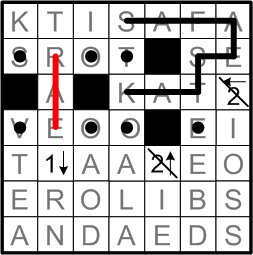As we did two steps earlier, we note that the dotted square between two blackened squares has but a single way to participate in the loop.
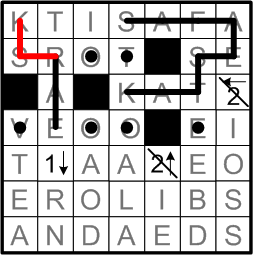Of course, there are other ways for dotted squares to be situated such that they can only participate in the loop in one way. The “S” square on the left edge of the grid provides another example.
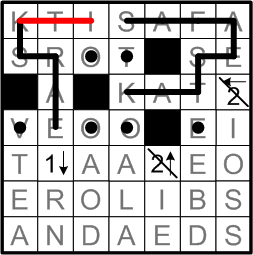We may then deduce some extension of that bit of the loop.
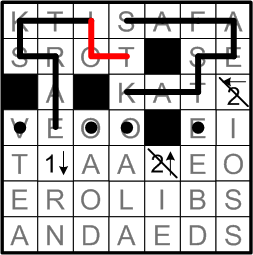Now, the “O” in the second row provides yet another example of a dotted square that must participate in the loop in a specific fashion.
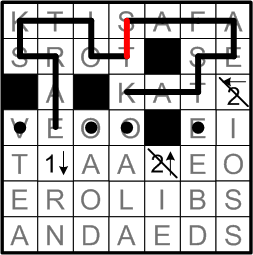And that leaves just one way for our original piece of the loop to continue: linking up all of our sub-path progress to date into a single strand.
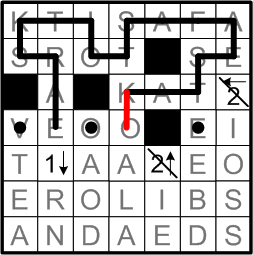Like dominoes falling, each triggering the movement of the next, the prior step now leads us to find only one way to extend the other end of our original piece of the loop.
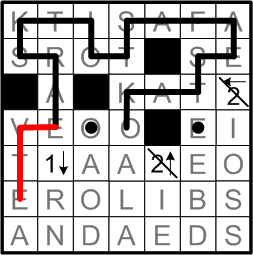The “V” square on the left edge of the grid provides our next example of a dotted square in a kind of “corder” situation. Because of the “1”-arrowed square, we are forced to extend our path a bit longer than in earlier corners.
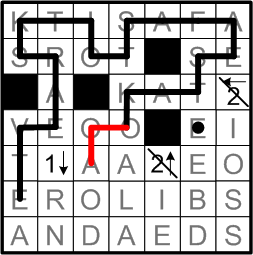Again we find a cascading series of deductions: the “V”-corner progress in the previous step leads now to similar progress in the corner occupied by the left-hand “O” square in the same row.
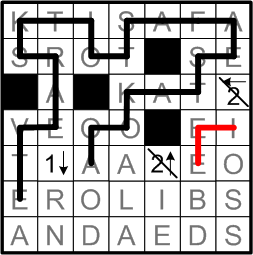We wrap up this series of “corner” deductions with the “E” square near the right end of that same row.
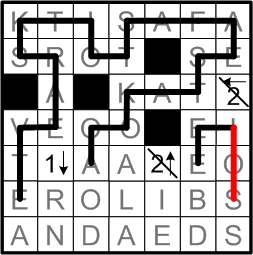Of course, we can then extend our latest piece of the loop a bit further, as we ensure that it does not close on itself before joining up with all of the rest.
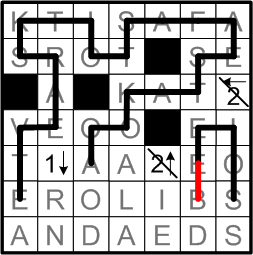Actually, that leads to even more such closing-avoidance progress.
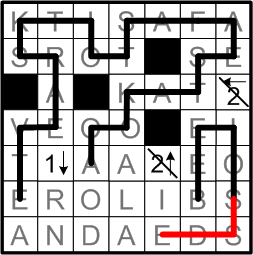And more progress still!
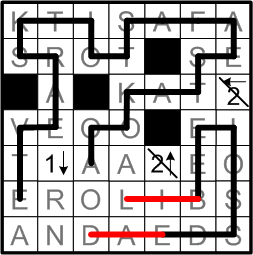Enough of this doling out progress in dribs and drabs! Here we fill in the full extent of this chain of deductions avoiding a premature closing.
We now must make a less-trivial deduction, similar in flavor to the one with which we began all of our work. Could the indicated “N” square be blackened? If it were, then the “A” square to its left would be (a) required to participate in the loop, but (b) completely unable to do so, having only one neighbor with which to do so.
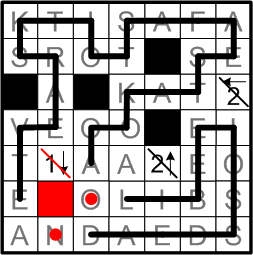We thus conclude that the black square indicated by the “1” arrow must not occupy the “N” sqaure, leaving only one alternative.
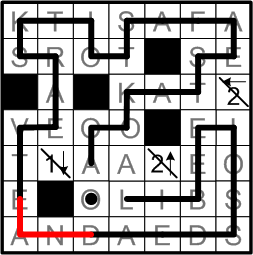The loop fragment running down the left edge of the grid now has but a single way to proceed.
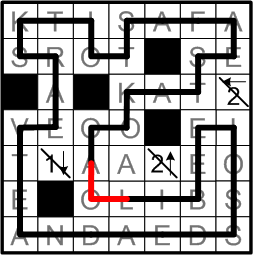The “O” square in the second-to-last row now provides our final example of the corner-deduction pattern.
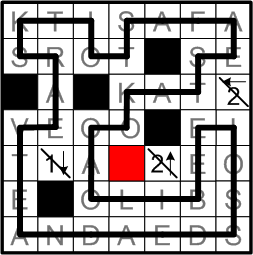This leaves only one possible fate for the as-yet-unmarked “A” square in the fifth row: it must needs be blackened!
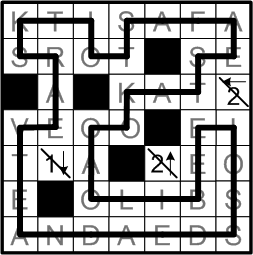Here we pause for just a moment to savor our completed grid.
All that remains now is to discover this ænigma's final answer.
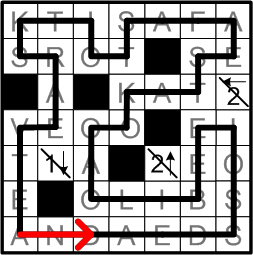We are told to walk our completed loop in an anticlockwise direction (as shewn by the arrow in the diagram), noting the letters occupying each square where our path makes a right-hand turn.
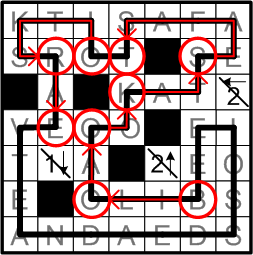Following those instructions, we end up spelling out a plainly apropos final answer: “BOOKSTORE”.
Bravo, we've done it! Now return to your efforts on the original ænigma!